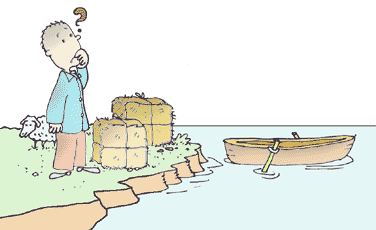
Curiosidade: Um problema de espaço!

Este agricultor está com um problema!

Precisa atravessar o rio para transportar sua carga que são dois fardos de capim e um carneiro. O problema é que ele só pode transportar uma coisa de cada vez no seu pequeno barco. Pior ainda, se ele deixar o carneiro e o capim juntos, o carneiro vai comer o mesmo.

Como fazer então para que ele leve sua carga para a outra margem sem prejuízo algum?

Fonte: http://matematica-legal.zip.net/ acessado no dia 05/07/10.

Curiosidade: Caleidoscópio.

Acesse o jogo abaixo e teste suas habilidades visuais:

http://www.testesdeqi.com.br/jogo/caleidoscopio/

Curiosidade: Futebol da tabuada

Quer fazer gols? Basta saber a tabuada... melhor ainda se souber as regras de divisibilidade. Veja se você é um craque acessando o link abaixo:

http://revistaescola.abril.com.br/matematica/pratica-pedagogica/jogo-tabuada-428051.shtml?comments=yes

Boa sorte!

Curiosidade: Copa de 2010 é da Alemanha?

O Brasil ganhou a copa do mundo em 1994, antes disso, sua última conquista do título foi em 1970.

Se você somar 1970 + 1994 = 3964

A Argentina ganhou a copa em 1986, antes em 1978.

Somando 1978 + 1986 = 3964

Já a Alemanha ganhou a copa em 1990. Antes disso foi em 1974.

Somando 1990 + 1974 = 3964

O Brasil ganhou a copa do mundo de 2002 e também foi vencedor da copa de 1962.

Conferindo: 1962 + 2002 = 3964

Seguindo esta lógica o ganhador da Copa de 2010 será o mesmo que em 1954.

Somando 2010 + 1954 = 3964

A Copa do Mundo em 1954 foi vencida pela Alemanha!

Será que vai funcionar?

Espero que não!

Fonte: http://celiaentreparenteses.blogspot.com/2010/01/copa-do-mundo-curiosidade-matematica.html acessado no dia 21/06/10.

Desafio para NÍVEL 2 (7ª e 8ª série)

Responda e depois verifique sua solução no vídeo anexado.

O lava-rápido "Lave Bem" faz uma promoção: Lavagem simples R$ 5,00; Lavagem completa R$ 7,00. No dia da promoção, o faturamento do lava-rápido foi de R$ 176,00. Nesse dia, qual o menor número possível de clientes que foram atendidos?

(a) 23 ............... (b) 24 ............... (c) 26 ............... (d) 28 ............... (e) 30

Fonte: http://www.orm.mtm.ufsc.br/, treinamento 4, nível 2, exercício 3, acessado no dia 16/06/2010.

Desafio para NÍVEL 1 (5ª e 6ª série)

Responda e verifique sua resposta no vídeo a seguir.

Um grupo de amigos acampou durante seis noites e, toda noite, dois deles vigiaram o acampamento. Cada um ficou de guarda três vezes, nunca com o mesmo amigo. Quantos eram os amigos?

(a) 3 ............... (b) 4 ............... (c) 6 ............... (d) 12 ............... (e) 18

Fonte: http://www.orm.mtm.ufsc.br/, treinamento 4, nível 1, exercício 1 acessado no dia 16/06/2010.

Desafio para NÍVEL 2 (7ª e 8ª série)

Resolva, justifique e comente:

Qual o maior resultado que podemos encontrar quando dividimos um número de 2 algarismos pela soma de seus algarismos?

Fonte: Caderno da OBMEP - Banco de questões 2009.

Desafio para NÍVEL 1 (5ª e 6ª série)

Resolva, justifique e comente:

Qual operação devemos fazer com todos os 5 números 418, 244, 816, 426, 24 para obter 5 números que tenham todos o algarismo 2?

(a) dividir 2 ..... (b) somar 4 ..... (c) dividir por 6 ..... (d) subtrair 5 ..... (e) multiplicar por 3

Fonte: Caderno da OBMEP - Banco de questões 2009

Curiosidade: Dicas para cálculos

Aí vai algumas dicas para você utilizar em seus cálculos:

DICA 1) Multiplicar um número por 10: basta deslocar a vírgula uma casa decimal para a direita.
Exemplo: a) 16 x 10 = 160 ....... b) 15,56 x 10 = 155,6 ...... c) 51,3 x 10 = 13

DICA 2) Dividir um número por 10: basta deslocar a vírgula uma csa decimal para a esquerda.
Exemplo: a) 16 : 10 = 1,6 ....... b) 15,56 : 10 = 1,556 ....... c) 51,3 : 10 = 5,13

DICA 3) Multiplicar um número por 9: nesse caso basta acrescentar um zero no final do número e subtrair pelo número inicial.

Exemplo: 44 x 9

- Acrescentando um zero: 440

- Subtraindo o valor inicial: 440 - 44 = 396 ..... ou seja, 44 x 9 = 396

Outro exemplo: 56 x 9 = 560 - 56 = 504

Fonte: http://www.somatematica.com.br/ acessado no dia 10/06/2010.

Desafio para NÍVEL 1 (5ª e 6ª série) e NÍVEL 2 (7ª e 8ª série)

Responda, justifique e comente:

Em cada uma das oito casas brancas do quadro dado, escrevemos um algarismo dentre os algarismos 1, 2, 3, 4, 5, 6, 7, 8 e 9 de modo que os produtos efetuados em linha reta, seguindo as flechas, forneçam os valores indicados dentro das casas em cinza. Em qual casa se encontra o número 2?

Fonte: Caderno da OBMEP - Banco de questões 2010.

Temos participantes!

Muito legal ter a participação de vocês nesse blog. Alguns alunos já postaram seus comentários. Poste você também!

A OBMEP ainda não acabou. Agora temos a segunda fase e quem faz parte dela terá mais um dia de competição. Quem não passou da primeira pode ficar torcendo e ajudando o seu colega que passou.

Bom estudo a todos!

Curiosidade: Jogar pedras no lago

A brincadeira de jogar pedras no lago e vê-las quicar ganhou base científica. Físicos da Universidade de Lyon, França, concluíram que a rocha pula mais se bater na água em um ângulo de 20 graus. Para isso, eles construíram uma máquina de arremesso de pedras e registraram tudo com uma câmara de alta velocidade.

Fonte: www.pet.mtm.ufsc.br/vocesabia.html acessado no dia 09/06/2010.

Desafio para NÍVEL 2 (7ª e 8ª série)

Responda, justifique e comente:

Se x + y = 8 e xy = 15, qual é o valor de x^2 + 6xy + y^2?

Obs: x^2 significa x ao quadrado, ou seja, x elevado à segunda potência. O mesmo acontece para y^2.

Fonte: http://www.orm.mtm.ufsc.br/, 5º treinamento, nível 2, 2010, acessado no dia 09/06/2010.

Desafio para NÍVEL 1 (5ª e 6ª série)

Responda, justifique e comente:

Se 1/8 de um número é 1/5, quanto vale 5/8 desse número?

Fonte: http://www.orm.mtm.ufsc.br/, 5º treinamento, nível 1, 2010, acessado no dia 09/06/2010.

Prova da 1ª fase, HOJE!

Leia a prova com muita atenção e utilize tudo que você conhece para resolvê-la.

Que você tenha bons resultados!

Curiosidade: Matemático Euclides

Para conhecer um pouco sobre a biografia do matemático grego Euclides, acesse o endereço www.somatematica.com.br/biograf/euclides.php.

Desafio para NÍVEL 2 (7ª e 8ª série)

Responda, justifique e comente.

Um antigo método para codificar palavras consiste em escolher um número de 1 a 26, chamado chave do código, e girar o disco interno do aparelho ilustrado na figura até que essa chave corresponda à letra A. Depois disso, as letras da palavra são substituídas pelos números correspondentes, separados por tracinhos. Por exemplo, na figura abaixo a chave é 5 e a palavra PAI é codificada como 20-5-13.

(a) Usando a chave indicada na figura, descubra qual palavra foi codificada como 23-25-7-25-22-13.

(b) Codifique OBMEP usando a chave 20.

(c) Chico codificou uma palavra de 4 letras com a chave 20, mas esqueceu-se de colocar os tracinhos e escreveu 2620138. Ajude o Chico colocando os tracinhos que ele esqueceu e depois escreva a palavra que ele codificou.

Fonte: Prova da OBMEP de 2007, 2ª fase, nível 2.

Desafio para NÍVEL 1 (5ª e 6ª série)

Responda, justifique e comente.

Para obter o resumo de um número de até 9 algarismos, deve-se escrever quantos são seus algarismos, depois quantos são seus algarismos ímpares e finalmente quantos são seus algarismos pares.

Por exemplo, o número 9103405 tem 7 algarismos, sendo 4 ímpares e 3 pares, logo seu resumo é 743.

(a) Encontre um número cujo resumo seja 523

(b) Encontre um número que seja igual ao seu próprio resumo.

Fonte: Prova da OBMEP de 2008, 2ª fase, nível 1.

Curiosidade: Adição e subtração

No site www.emundy.com/jogos_online/jogo.php?id=873 você recebe adições e subtrações para serem calculadas. Bom para exercitar o cálculo mental. Experimente!

Desafio para NÍVEL 2 (7ª e 8ª série)

Responda, justifique e comente:

As duas peças de madeira a seguir são iguais.

Pode-se juntar essas duas peças para formar uma peça maior, como mostra o seguinte exemplo:

Qual das figuras abaixo representa uma peça que NÃO pode ser formada com as duas peças dadas?

Fonte: Prova da OBMEP de 2005, 1ª fase e nível 2.

Desafio para NÍVEL 1 (5ª e 6ª série)

Responda, justifique e comente:

Guilherme está medindo o comprimento de um selo com um pedaço de uma régua, graduada em centímetros, como mostra a figura. Qual o comprimento do selo?

Fonte: Prova da OMBEP de 2005, 1ª fase e nível 1.

Curiosidade: Akinator - um gênio que usa a lógica

Akinator, um "gênio da web", saiu da garrafa em território nacional. Trata-se de uma brincadeira. O internauta pensa em um personagem - vivo, morto, ficcional, familiar - e responde acerca de 15 perguntas. São cinco alternativas de resposta.

No fim, o gênio Akinator, baseado na lógica, tenta apontar em quem a pessoa pensou.

Para acessar o site do gênio, clique em www.akinator.com

Fonte: http://matematicamania.wordpress.com/category/curiosidades/ acessado no dia 02/06/2010.

Desafio para NÍVEL 1 (5ª e 6ª série) e NÍVEL 2 (7ª e 8ª série)

Responda, justifique e comente:

Um pai tem 14 presentes, distribuídos em envelopes lacrados contendo 1, 2, 3, ..., 14 chocolates, respectivamente, que ele pretende distribuir entre suas filhas Alice, Beatriz e Camila, de modo que cada uma das filhas receba a mesma quantidade de chocolates. Como o pai pode fazer essa distribuição? Dê mais de uma possibilidade.

E se em vez de 14 fossem 13 envelopes contendo 1, 2, 3, ..., 13 chocolates, respectivamente?

Fonte: Olimpíada de Matemática do Rio Grande do Norte de 2008.

Curiosidade: O jogo dos 11

Quer jogar? Convide um colega.

Nesse jogo participam 2 jogadores. Colocam-se sobre uma mesa 11 caroços de feijão. Os dois jogam alternadamente. O primeiro jogador retira um, dois ou três caroços, a quantidade a sua escolha. O segundo jogador retira um, dois ou três caroços, de acordo com sua vontade. Em seguida joga o primeiro com as regras estabelecidas, e assim por diante. Não se pode retirar mais que três caroços de uma vez. O que retirar o último caroço perde.

Como você deverá jogar para ganhar o jogo?

Fonte: www.olimpiada.ccet.ufrn.br/treinamento_2004/nota_aula_02.pdf acessado no dia 01/06/2010.

Desafio para NÍVEL 2 (7ª e 8ª série)

Resolva, justifique e comente:

Na figura, temos o ângulo B igual a 50°, sendo AD e CD as bissetrizes dos ângulos A e C, respectivamente. Qual é a medida do ângulo ADC?

Fonte: Caderno da OBMEP - Banco de questões 2010.

Desafio para NÍVEL 1 (5ª e 6ª série)

Responda, justifique e comente:

O número 10 pode ser escrito de duas formas diferentes como soma de dois número primos: 10=5+5 e 10=3+7. De quantas maneiras podemos expressar o número 25 como uma soma de dois números primos?

(A) 1 .......... (B) 2 .......... (C) 3 .......... (D) 4 .......... (E) nenhuma

Fonte: www.coladaweb.com/matematica/exercicios-de-numeracao acessado no dia 01/06/2010.

Curiosidade: Você sabia?

No site http://www.somatematica.com.br/ são oferecidos jogos matemáticos muito divertidos. Um deles é o "Decifre o Enigma". Neste jogo você deve analisar duas frases e uma figura. Com elas você pensa e escreve a resposta correta.

Experimente! Entre no site e clique no link "Jogos Matemáticos" que fica no "Entretendimentos".

Boa sorte!

Desafio para NÍVEL 2 (7ª e 8ª série)

Responda e verifique sua resposta no vídeo abaixo:

Devido a um defeito de impressão, um livro de 600 páginas apresenta em branco todas as páginas cujos números são múltiplos de 3 ou de 4. Quantas páginas estão impressas?

(a) 100 ..... (b) 150 ..... (c) 250 ..... (d) 300 ..... (e) 430

Resolução no vídeo:

Fonte: www.orm.mtm.ufsc.br/arquivos/treinamentos/2010/02lista03.pdf acessado no dia 27/05/2010.

Desafio para NÍVEL 1 (5ª e 6ª série)

Responda e depois verifique a solução no vídeo abaixo.

Sabendo-se que 9174532 . 13 = 119268916, pode-se concluir que é divisível por 13 o número:

(a) 119268903 ..... (b) 119268907 ..... (c) 119268911 ..... (d) 119268913 ..... (e) 119268923

Vídeo com a resolução:

Fonte: www.orm.mtm.ufsc.br/arquivos/treinamentos/2010/01lista02.pdf acessado no dia 27/05/2010.

Curiosidade: 2 é igual a 1?

Tente descobrir o que tem de estranho!

Fonte: www.somatematica.com.br/absurdos/doisigualaum.php acessado no dia 26/05/2010.

Desafio para NÍVEL 1 (5ª e 6ª série) e NÍVEL 2 (7ª e 8ª série)

Responda, justifique e comente:

Os números de 1 a 9 foram colocados dentro de cinco anéis olímpicos, de tal modo que dentro de cada anel a soma é 11.

Disponha os nove números de outra maneira, para que a soma dentro de cada anel seja sempre a mesma e a maior possível.

Fonte: Caderno da OBMEP - Banco de questões 2010.

Curiosidade: Pérolas da matemática

1) Simplificação de radicais:

2)

Fonte: minhas anotações.

Desafio para NÍVEL 1 (5ª e 6ª série) e NÍVEL 2 (7ª e 8ª série)

Responda, justifique e comente:

Três amigos entraram numa pousada, pediram ao proprietário que fritasse alguns pastéis e foram tirar um cochilo. O proprietário levou uma travessa de pastéis para o quarto, colocou sobre a mesa e saiu sem fazer barulho. Passado algum tempo, um dos amigos acordou, viu os pastéis e, sem acordar os companheiros, contou quantos havia, comeu um terço e dormiu de novo. Logo depois, o segundo amigo acordou. Sem saber que o primeiro já havia comido sua parte, contou os pastéis da travessa, comeu um terço e voltou a dormir. Finalmente o terceiro despertou. Contou os pastéis e comeu um terço. Nesse momento, os dois primeiros rapazes acordaram e o mal entendido foi resolvido. Sabe-se que na travessa ainda restavam 8 pastéis. Descubra:

a) quantos pastéis o proprietário da pousada fritou?

b) quantos pastéis cada um dos rapazes comeu?

c) quantos pastéis cada um deveria comer a mais para que os três se servissem da mesma quantidade?

Fonte: http://magiadamatematica.com/diversos/curiosidades/17-desafie-o-seu-raciocinio-1.pdf acessado no dia 25/05/2010.

Curiosidade: OBMEP

A prova da primeira fase está chegando. Aproveite para fazer uma visita ao site da olimpíada:

http://www.obmep.org.br/

Desafio para NÍVEL 1 (5ª e 6ª série) e NÍVEL 2 (7ª e 8ª série)

Responda, justifique e comente:

De quantos modos diferentes podemos escrever o número 497 como a soma de dois números naturais primos?

Fonte: http://magiadamatematica.com/diversos/curiosidades/17-desafie-o-seu-raciocinio-1.pdf acessado no dia 24/05/2010.

Curiosidade: Ilusão de ótica

Fixe sua vista no ponto azul por 20 segundos. Depois mire seus olhos em uma parede branca e verás a Bandeira Brasileira com todas as suas cores.

Fonte: http://magiadamatematica.com/diversos/curiosidades/07-ilusao-de-otica.pdf acessado no dia 21/05/2010.

Desafio para NÍVEL 2 (7ª e 8ª série)

Na figura abaixo temos dois quadrados. O maior tem lado a + b e o menor lado a. Qual é a área da região em cinza?

Fonte: Caderno da OBMEP - Banco de questões 2006.

Desafio para NÍVEL 1 (5ª e 6ª série)

Na malha quadriculada a seguir, todas as circunferências têm o mesmo centro. Então, pode-se concluir que a área cinza é:

A) Dois quintos da área do círculo maior.
B) Três sétimos da área do círculo maior.
C) Metade da área do círculo maior.
D) Quatro sétimos da área do círculo maior.
E) Três quintos da área do círculo maior

Fonte: Caderno da OBMEP - Banco de questões 2006.

Curiosidade: O matemático e o motorista.

Aquele matemático famoso estava a caminho de uma conferência quando o seu motorista comentou:

- Patrão, já ouvi tantas vezes a sua palestra que tenho certeza de que poderia fazê-lo no seu lugar, se o senhor ficasse doente.

- Isso é impossível!

- Quer apostar?!

E fizeram a aposta! Trocaram de roupa, e quando chegaram ao local da conferência o motorista foi para a Tribuna enquanto o matemático instalou-se na última fila, como se fosse seu motorista.

Depois da palestra, começou a sessão de perguntas, que ele respondeu com precisão. No entanto, em certo momento, levantou-se um sujeito que apresentou uma questão dificílima. Longe de entrar em pânico, ele saiu com esta:

- Meu jovem, essa pergunta é tão fácil... mas, tão fácil... que vou pedir para o meu motorista responder!

Fonte: http://magiadamatematica.com/diversos/curiosidades/12-humor-na-matematica1.pdf acessado no dia 20/05/2010.

Desafio para NÍVEL 1 (5ª e 6ª série) e NÍVEL 2 (7ª e 8ª série)

Responda, justifique e comente:

Sofia foi levar uns docinhos para sua avó; são 7 docinhos de amora, 6 de côco e 3 de chocolate. Durante o caminho, a gulosa Sofia come 2 docinhos. Qual das situações abaixo é possível?

(A) Vovó não recebeu docinhos de chocolate.

(B) Vovó recebeu menos docinhos de côco do que de chocolate.

(C) Vovó recebeu o mesmo número de docinhos de cada uma das 3 variedades.

(D) Existem 2 variedades de docinhos das quais vovó recebeu o mesmo número.

(E) O número de docinhos de amora que vovó recebeu é maior que os outros 2 somados.

Fonte: Caderno da OBMEP - Banco de questões 2009.

Curiosidade: Relógios (quase) infalíveis

"Funciona como um relógio". Você já ouviu essa expressão? É usada para se referir a alguma coisa que funciona direitinho, com regularidade a toda prova.

O relógio atômico é movido pela radioatividade emitida por uma pedra de césio. Ele mede o tempo em nanossegundos (ou um bilionésimo de segundos). Mas, mesmo assim, atrasa 1 segundo a cada 3 milhões de anos!

Melhor que ele só o relógio mais preciso do mundo, desenvolvido por uma equipe de cientístas alemães e americanos. Ele usa um átomo de mercúrio como combustível, e conta com a ajuda de um raio laser.

Esse super relógio divide um segundo em um quatrilhão: os femtossegundos. O mais incrível é que ele só atrasa 1 segundo a cada 3 bilhões de anos!

Fonte: www.canalkids.com.br/cultura/matematica/curiosidades.htm

Desafio para NÍVEL 2 (7ª e 8ª série)

Responda, justifique e comente:

Existe um número inteiro N tal que 2008 x N = 222...2?

Fonte: Caderno da OBMEP - Banco de questões 2008

Desafio para NÍVEL 1 (5ª e 6ª série)

Responda, justifique e comente:

As formiguinhas Maricota e Nandinha passeiam numa varanda cujo chão é formado por lajotas retangulares de 4 cm de largura por 6 cm de comprimento. Maricota parte do ponto M e Nandinha do N, andando ambas apenas pelos lados dos retângulos, percorrendo o trajeto no sentido indicado na figura.

a) As duas se encontram depois de andarem a mesma distância. Qual foi essa distância?

b) Aonde elas se encontraram?

Fonte: Caderno da OBMEP - Banco de questões 2008.

Curiosidade: Matemática e arte!

Vejam lindas figuras no site: http://vodpod.com/watch/1114155-matemtica-e-arte, acessado no dia 18/05/2010.

Desafio para NÍVEL 1 (5ª e 6ª série) e NÍVEL 2 (7ª e 8ª série)

Tente e comente:

Reparta um quadrado em sete quadrados menores.

Fonte: Caderno da OBMEP - Banco de questões 2010.

Curiosidade: Regra de três!

A regra de três é um assunto importantíssimo na matemática. Com ela, resolvemos boa parte dos problemas matemáticos que surgem no nosso dia a dia. Mas, antes de apresentar um exemplo usando a regra de três, vamos brincar um pouquinho.

O desafio é partir de uma palavra para chegar em outra. Durante a brincadeira só podem surgir palavras conhecidas quando trocarmos uma letra por outro. Somente uma letra de cada vez.

Exemplo: partindo da palavra TERRA para chegarmos na palavra MARTE.

TERRA (trocar E por O) - TORRE (trocar T por M) - MORRE (trocar R por T) - MORTE (trocar O por A) - MARTE.

Treinem um pouquinho: 1) Partir de LIXO e chegar em OURO; 2) Partir de PENA e chegar em AMOR; 3) Partir de DROGA e chegar em SAÚDE.

Para resolvermos um exercício por regra de três podemos usar a mesma idéia. Vejamos dois exemplos:

Exemplo 1) Uma padaria produz 400 pães com 10 kg de farinha de trigo. Quantos pães ela produzirá com 15 kg de farinha de trigo?

Temos a quantidade de pães para 10 kg de farinha de trigo, como queremos saber de 15 kg, basta trocar 10 por 15 (como na brincadeiras das palavras, mas usando operações de multiplicação e divisão): 10 x 3 = 30 e 30 : 2 = 15 (multiplicamos por 3 e depois dividimos por 2). Como as grandezas são diretamente proporcionais (com mais farinha faremos mais pães), façamos com o número de pães a mesma coisa: 400 x 3 = 1200 e 1200 : 2 = 600. Ou seja, com 15 kg de farinha a padaria irá produzir 600 pães.

Exemplo 2) Uma padaria gasta 10 horas para fazer a produção diária de pães, utilizando 3 padeiros. Quantas horas diárias esta padaria gastaria se tivesse 5 padeiros?

Temos a quantidade de horas para 3 padeiros, como queremos saber para 5, basta trocar 3 por 5. uma sugestão: 3 x 5 = 15 e 15 : 3 = 5 (primeiro multiplicamos por 5 e depois dividimos por 3). Como as grandezas são inversamente proporcionais (com mais padeiros gastaremos menos tempo), façamos com o número de horas o inverso: 10 : 5 = 2 e 2 x 3 = 6. Ou seja, com 5 padeiros a padaria irá gastar 6 horas.

Fonte: www.scribd.com/doc/4074678/Matematica-PPT-Regra-de-Tres acessado no dia 17/05/2010.

Desafio para NÍVEL 1 (5ª e 6ª série) e NÍVEL 2 (7ª e 8ª série)

Responda, justifique e nos envie:

Numa família, cada menino tem o mesmo número de irmãos que de irmãs, e cada menina tem o dobro de irmãos que de irmãs. Qual é a composição dessa família?

Fonte: Caderno da OBMEP - Banco de questões 2010.

Curiosidade: Raiz quadrada fácil!

Um vídeo do youtube mostra o cálculo de raiz quadrada de uma forma diferente. Vale a pena conferir: http://www.youtube.com/watch?v=F2vjZ8M-K1Q acessado no dia 14/05/2010.

Desafio para NÍVEL 1 (5ª e 6ª série) e NÍVEL 2 (7ª e 8ª série)

Resolva, justifique e comente:

Amélia, Bruno, Constância e Denise são quatros amigos que se encontram sentados numa mesa quadrada, cada um ocupando um lado da mesa. Um dos quatro mora no Amazonas, outro em São Paulo, outro no Ceará e o quarto na Bahia. Sabendo que valem as condições a seguir, quem mora na Bahia?

• À direita de Amélia está quem mora no Amazonas.
• Em frente à Constância está a pessoa que mora em São Paulo.
• Bruno e Denise estão um ao lado do outro.
• Uma mulher está à esquerda da pessoa que mora no Ceará.

Fonte: Caderno da OBMEP - Banco de questões 2010.

Curiosidade: Os números negativos.

Brahmagupta, matemático nascido no ano 598 d.C., afirmava que os números podem ser entendidos como pertences ou dívidas.

Mas, sem símbolos próprios para que se pudesse realizar as operações, os números absurdos, como eram chamados, não conseguiam se firmar como verdadeiros números.

Depois de várias tentativas frustadas, os matemáticos conseguiram encontrar um símbolo que permitisse operar com esse novo número. Mas como a história da matemática é cheia de surpresas, não poderia de faltar mais uma:

Ao observar a prática adotada pelos comerciantes da época, os matemáticos verificaram que se no início do dia, um comerciante tinha em seu armazém duas sacas de feijão de 40 quilogramas cada e se até o final do dia ele tivesse vendido 7 quilogramas, ele escrevia o número 7 com um tracinho na frente (-7). Isso o lembraria que naquele saco de feijão tem 7 quilogramas a menos que a quantidade inicial. Mas se ele resolvesse despejar no outro saco 3 quilogramas, escrevia o número 3 com dois tracinhos cruzados na frente (+3), para se lembrar que naquele saco havia 3 quilogramas a mais de feijão do que a quantidade inicial.

Os matemáticos aproveitaram-se desse expediente e criaram o número com sinal: positivo (+) ou negativo (-).

Fonte: www.imagick.org.br/zbolemail/Bol03x12/BE12x10.html acessado no dia 13/05/2010.

Desafio para NÍVEL 2 (7ª e 8ª série)

Responda, justifique e nos envie:

Uma loja de sabonetes realiza uma promoção com o anúncio "Compre um, leve outro pela metade do preço". Outra promoção que a loja poderia fazer oferecendo o mesmo desconto percentual é:

(a) leve dois, pague um

(b) leve três, pague um

(c) leve três, pague dois

(d) leve quatro, pague três

(e) leve cinco, pague quatro

Fonte: http://www.orm.mtm.ufsc.br/, 3ª lista de treinamentos de 2010, nível 2, acessado no dia 13/05/2010.

Desafio para NÍVEL 1 (5ª e 6ª série)

Responda, justifique e nos envie:

Com segmentos de 1cm de comprimento podemos formar triângulos. Por exemplo, com nove desses segmentos podemos formar um triângulo equilátero de lado 3 cm. Com qual número de segmentos a seguir é impossível formar um triângulo?

(a) 4 .......... (b) 5 .......... (c) 6 .......... (d) 7 .......... (e) 8

Fonte: http://www.orm.mtm.ufsc.br/, 3ª lista de treinamentos de 2010, nível 1, acessado no dia 13/05/2010.

Curiosidade: Origami

Origami é a arte tradicional japonesa de dobrar papel, criando representações de determinados seres ou objetos com as dobras geométricas de uma peça de papel, sem cortá-la ou colá-la.

Vejamos alguns origamis:

Fonte: http://pt.wikipedia.org/wiki/Origami

Desafio para NÍVEL 2 (7ª e 8ª série)

Responda, justifique e comente:

Truque numérico:

(i) escolhaum número qualquer
(ii) multiplique-o por 6
(iii) do resultado subtraia 21
(iv) divida esse novo resultado por 3
(v) desse último resultado subtraia o dobro do número que você escolheu

Experimente essa sequência de cinco passos três vezes, iniciando cada vez com um número diferente. Verifique resultado e depois, usando a letra x para representar um número qualquer, mostre porque os resultados não são apenas uma coincidência, mas sim um fato matemático.

Fonte: Caderno da OBMEP - Banco de questões 2010.

Desafio para NÍVEL 1 (5ª e 6ª série)

Responda, justifique e comente:

Nove amigos compraram três bolos, cada um deles cortado em oito fatias. Todos comeram bolo e não sobrou nenhum pedaço. Sabendo que cada um só comeu fatias inteiras do bolo, podemos ter certeza de que:

(A) alguém comeu quatro fatias;
(B) um deles comeu somente uma fatia;
(C) todos comeram duas fatias, pelos menos;
(D) uns comeram duas fatias e os demais comeram três fatias;
(E) um deles comeu, no mínimo, três fatias.

Fonte: Caderno da OBMEP - Banco de questões 2010.

Curiosidade: A Matemática na música

Acesse o link http://www2.tvcultura.com.br/artematematica/prog08.html (11/05/2010)

Desafio para NÍVEL 2 (7ª e 8ª série)

Responda, justifique e comente:

Uma classe tem 22 alunos e 18 alunas. Durante as férias, 60% de todos os alunos dessa classe foram prestar trabalho comunitário. No mínimo, quantas alunas participaram desse trabalho?

Fonte: http://www.orm.mtm.ufsc.br/, 2º treinamento, nível 2, acessado no dia 11/05/2010.

Desafio para NÍVEL 1 (5ª e 6ª série)

Responda, justifique e comente:

Pedro vendia na feira, cenouras a R$ 1,00 por quilo e tomates a R$ 1,10 por quilo. Certo dia ele se distraiu, trocou os preços entre si e acabou vendendo 100 quilos de cenoura e 120 quilos de tomate pelos preços trocados. Quanto ele deixou de receber por causa de sua distração?

Fonte: http://www.orm.mtm.ufsc.br/, 2º treinamento, nível 1 acessado no dia 11/05/2010.

Visita à Escola Básica Professora Adriana Weingartner

Estiveram presentes, aproximadamente, 40 alunos no encontro da OBMEP na escola Adriana. Foi conversado sobre as regras da olimpíada, sobre curiosidades e exercícios. Os alunos participaram bastante.

Parabéns a todos e boa prova da 1ª fase!

Curiosidade: O número PHI

A diferença entre o PHI e o PI é muito mais que só o H. O número PHI, representado pelo número 1,618 é muito importante na arte. O PHI é geralmente considerado o número mais belo do mundo. Este número vem da série de Fibonacci - uma progressão famosa não só porque a soma dos termos adjacentes equivalia ao termo seguinte, mas porque os quocientes dos termos adjacentes possuíam a estaeecedora propriedade de irem se aproximando gradativamente do número 1,618, o PHI.

Apesar das origens matemáticas aparentemente místicas do PHI, o aspecto surpreendente do PHI foi seu papel como componente básico na Natureza. Plantas, animais e até seres humanos - todos possuíram propriedades dimensionais que se encaixavam com uma exatidão espantosa à razão de PHI para um. A unipresença do PHI na natureza está além da coincidência, e assim os antigos presumiram que o número PHI deve ter sido predeterminado pelo Criador do universo. Os primeiros cientístas solenemente anunciaram que o número um vírgula seis um oito era a Divina Proporção.

Exemplos:

1) Se você dividir o número de abelhas fêmeas pelo número de abelhas machos em qualquer colméia do mundo, vai sempre obter o mesmo número: PHI, 1,618.

2) Um miolo de flor de girassol. As sementes de girassol crescem em espirais opostas. A razão de cada rotação para a seguinte é de 1,618, PHI.

Leonardo Da Vince foi o primeiro a demonstrar que o corpo humano é literalmente feito de componentes cujas razões proporcionais sempre equivalem a PHI.

3) A distância de um ombro até a ponta dos dedos dividido pela distância entre o cotovelo até a ponta dos dedos é PHI, 1,618.

Fonte: www.somatematica.com.be/curiosidades/c28.html

Desafio para NÍVEL 2 (7ª e 8ª série)

Responda, justifique e comente:
Qual dos números a seguir está mais próximo de ?

(A) 0,03 ....... (B) 0,3 ....... (C) 3 ....... (D) 30 ....... (E) 300

Fonte: http://www.obmep.org.br/ nos links Provas 2007, 1ª fase, nível 2, acessado no dia 10/05/2010.

Desafio para NÍVEL 1 (5ª e 6ª série)

Resolva, justifique e comente:

Um número par tem 10 algarismos e a soma desses algarismos é 89. Qual é o algarismo das unidades desse número?

Fonte: http://www.obmep.org.br/ nos links Provas 2007, 1 fase, nível 1, acessado no dia 10/05/2010.

Curiosidade: Problema de Malba Tahan

A seguir, para continuar a homenagem do dia de ontem (dia da Matemática), um problema clássico de Malba Tahan.

Durante uma calorosa discussão entre três irmãos, eis que surgem dois amigos montados num camelo que não conseguiram evitar uma paragem para apaziguar tal discussão. A falta de entendimento entre aqueles homens devia-se ao fato de não conseguirem fazer a divisão da herança de seu pai - 35 camelos. Não havia forma de chegarem a um consenso.

Segundo a vontade expressa do falecido, metade da herança seria para o seu filho mais velho, uma terça parte para o filho Hamed e, finalmente, para o filho mais novo, Harim, resta a nona parte da herança.

O filho mais velho pede 18 camelos, uma vez que metade de 35 são 17,5. Esta pretensão não foi aceita pelos outros irmãos, dado que o mais velho já leva a metade da herança. Hamed tendo direito a uma terça parte, 11 camelos e ainda mais de metade de outro, com toda a justiça acha que deve ficar com 12 camelos. Mas, Harim discorda completamente porque segundo a vontade de seu pai a nona parte da herança são quase 4 camelos. Dado ser ele o que menos recebe, então o mais novo reclama para si o benefício do arredondamento à parte inteira mais próxima.

É nesta altura que intervém Beremiz - o homem que sabia contar, dizendo que o que mais incomoda é ver 3 irmãos a discutir um problema que é dos mais simples de resolver. Contra a vontade do seu companheiro de viagem, Beremiz fez questão em juntar à herança também o camelo em que eles se deslocavam, ficando, assim, 36 camelos para repartir pelos três irmãos.

Impávidos e já mais serenos, acreditando que se tratava de obra divina o aparecimento e a bondade de tal criatura, os três irmão aceitaram que fosse Beremiz, com justiça, a fazer a tal divisão.

Não havendo dúvidas que metade do conjunto de 36 camelos são 18, Hamed e Harim deixaram partir o seu irmão mais velho com o número de camelos que antes reclamara. Também Hamed ficou satisfeito, dado que uma terça parte de 36 era precisamente aquilo que ele pretendia, 12 camelos. Por fim, também Harim não se pode queixar, uma vez que a nona parte da nova herança dava-lhe direito a que ficasse com 4 camelos.

Concluindo, todos os irmãos saíram a lucrar com aquela divisão 18 + 12 + 4, fazendo um total de 34 camelos. Perante esse fato o companheiro de viagem de Beremiz nem queria acreditar como era possível aquele entendimento e agora poderem prosseguir a sua viagem montados cada um em seus camelo.

Você consegue compreender o que aconteceu?

Fonte: http://maismat.blogspot.com/2008/11/diviso-de-unidades-indivisiveis.html acessado no dia 07/05/2010.

Desafio para NÍVEL 2 (7ª e 8ª série)

Responda, justifique e comente:

Geni é cliente de uma companhia telefônica que oferece o seguinte plano:

• tarifa mensal fixa de R$ 18,00;
• gratuidade em 10 horas de ligações por mês;
• R$ 0,03 por minuto que exceder as 10 horas gratuitas.

Em janeiro, Geni usou seu telefone por 15 horas e 17 minutos e, em fevereiro, por 9 horas e 55 minutos. Qual foi adespesa de Geni com telefone nesses dois meses, em reais?

Fonte: Caderno da OBMEP - Banco de Questões 2010.

Desafio para NÍVEL 1 (5ª e 6ª série)

Responda, justifique e comente:

Uma farmácia dá desconto de 30% sobre o preço de tabela de todos os medicamentos que vende. Ao adquirir um remédio cujo preço de tabela é R$ 120,00, quantos reais uma pessoa irá pagar?

Fonte: Caderno da OBMEP - Banco de Questões 2010.

Curiosidade: DIA DA MATEMÁTICA!

A Sociedade Brasileira de Educação Matemática - SBEM elegeu o dia 06 de maio (hoje) como "DIA NACIONAL DA MATEMÁTICA", em memória da data de nascimento de Júlio César de Mello e Souza, o MALBA TAHAN.

Mas quem foi Malba Tahan?

Natural do Rio de Janeiro, filho de professores, nascido em 6 de maio de 1895 e falecido em 18 de junho de 1974, aos 79 anos (Recife). No colegial, mostrou-se hábil em suas redações, as quais vendia para comprar chocolates. Manteve, ainda no colegial, o seu primeiro jornal, o "Erre", com tiragem limitada a um único exemplar. Enquanto professor primário lecionou desde aos 18 anos em escolas particulares, oficiais e proficionais. Formou-se engenheiro (apesar do desejo do pai de que fosse militar) chegando ao Magistério Superior, tendo sido professor Catedrático e Emérito. Seguiu pela carreira literária, em 1918, desejando publicar seus contos no jornal carioca, com o pseudônimo de "Slady". Em 1932, lança a mais conhecida de suas obras, "O Homem que calculava" traduzido para o espanhol, inglês, alemão, italiano e esloveno. Em seus 50 anos de atividade literária publicou 120 livros, dos quais 51 referentes à Matemática.

Fonte: José Roberto Medeiros em http://crv.educacao.mg.gov.br/sistema_crv/banco_objetos_crv/%7BC1683E29-2FD7-44F3-A42A-452E43F27D acessado em 06/05/2010.

Desafio para NÍVEL 2 (7ª e 8ª série)

Responda, justifique e comente:

Qual é o algarismo da unidade do número 1 x 3 x 5 x 79 x 97 x 113?

Fonte: Caderno da OBMEP - Banco de Questões 2010

Desafio para NÍVEL 1 (5ª e 6ª série)

Responda, justifique e comente:

A figura dada representa um gramado retangular em que foram marcados sete quadrados numerados de 1 a 7. Se a área do menor desses quadrados é 1 metro quadrado, qual é a área total do gramado (em metros quadrados)?

Fonte: Caderno da OBMEP - Banco de Questões 2010.

Visita à Escola Básica Professor Neri Brasiliano Martins

Hoje (05/05) aconteceu o encontro da OBMEP com alunos da escola Neri. Estiveram participando, mais ou menos, 70 alunos (5ª a 8ª série). Estes foram muito receptivos e participativos. Falamos do regulamento da olimpíada, de curiosidades e de exercícios.

Obrigada e parabéns a todos vocês! Gostei bastante!

Tudo de bom para o dia 08/06/2010.

Curiosidade: O que é um número capicua.

Um número é capicua quando lido da esquerda para a direita ou da direita para a esquerda representa sempre o mesmo valor, como por exemplo, 77, 434, 6446, 82328. Para obter um número capicua a partir de outro, inverte-se a ordem dos algarismos e soma-se com o número dado, um número de vezes até que se encontre um número capicua, como por exemplo:

Partindo do número 84:

84+48=132 ..... 132+231=363 ..... que é um número capicua.

Fonte: www.somatematica.com.br/curiosidades.php

Desafio para NÍVEL 2 (7ª e 8ª série)

Responda, justifique e comente:

Um cachorro começa a perseguir um coelho que está dez metros a sua frente. Enquanto o coelho corre um metro, o cachorro corre dez metros. É correto afirmar que o cachorro:

(A) correrá exatamente dez metros até alcançar o coelho

(B) correrá mais que dez metros e menos que onze metros até alcançar o coelho

(C) correrá exatamente onze metros até alcançar o coelho

(D) correrá mais que onze metros e menos que doze metros até alcançar o coelho

(E) nunca alcançará o coelho

Fonte: http://www.obmep.org.br/ nos links Provas 2009, 1ª fase, nível 1, acessado no dia 05/05/2010.

Desafio para NÍVEL 1 (5ª e 6ª série)

Responda, justifique e comente:

Davi estava fazendo uma conta no caderno quando sua caneta estragou e borrou quatro algarismos, como na figura. Ele se lembra que só havia algarismos ímpares na conta. Qual é a soma dos algarismos manchados?

Fonte: http://www.obmep.org.br/ nos links Provas 2009, 1ª fase, nível 1, acessado no dia 05/05/2010.

Visita à Escola Básica Morretes II

Hoje, dia 04/05/2010, aconteceu o encontro sobre a OBMEP na escola do Morretes. Os 35 alunos, aproximadamente, de 5ª série ouviram sobre o regulamento, curiosidades na matemática e exercícios. Foi um encontro muito bom e bem proveitoso.

Obrigada a todos e que tenham uma boa olimpíada no dia 08 de junho.

Curiosidade: Teste do cérebro!

Foi descoberto que o nosso cérebro tem um Bug. Aqui vai um pequeno teste de cálculo mental! Este cálculo deve fazer-se mentalmente (e rapidamente), sem utilizar calculadora nem papel e caneta! Ah! Não veja a resposta antes defazer seu cálculo.

Lá vai: Tens 1000, acrescenta-lhe 40. Acrescenta mais 1000. Acrescenta mais 30 e novamente 1000. Acrescenta 20. Acrescenta 1000 e ainda 10.

Qual é o total?

O seu resultado é 5000?

Pois é... a resposta certa é 4100! Se não acreditar, verifique com a calculadora. O que acontece é que a sequência decimal confunde o nosso cérebro, que sobe naturalmente para a mais alta decimal (centenas em vez de dezenas).

Fonte: http://risotanosapo.blogs.sapo.pt/981.html

Desafio para NÍVEL 1 (5ª e 6ª série) e NÍVEL 2 (7ª e 8ª série)

Responda, justifique e comente:

O problema dos vasilhames

Como é possível retirar de um rio exatamente 6 litros de água dispondo apenas, para medir a água, de dois recipientes: um com 4 litros e o outro com 9 litros de capacidade?

Atenção: Os dois recipientes não tem marcas, isto é, não é possível colocar água até a metade do vasilhame.

Fonte: minhas anotações.

Visita à Escola Básica Professora Antonieta Silveira de Souza

No dia 03/05/2010 foi realizado um encontro com alunos da escola Antonieta para conversarmos sobre a OBMEP. Nessa conversa foi apresentado alguns ítens do regulamento da olimpíada, curiosidades e exercícios. Tivemos a participação de, aproximadamente, 30 alunos.

Obrigada a todos que participaram e boa prova no dia 08 de junho!

Curiosidade: Você é capaz de somar os algarismos de 1 a 100 em poucos minutos?

Carl Friedrich Gauss (1777-1855) aos 10 anos de idade respondeu rapidamente 5050 ao seu professor surpreendendo-o pela sua grande habilidade na matemática. Em 1792, seu talento foi reconhecido pelo duque de Braunschweig, que lhe garantiu recursos para prosseguir o estudo de matemática. Gauss criou a geometria diferencial, e fez novas descobertas como a Lei da Reciprocidade Quadrática, que introduz o conceito de congruência e o Teorema Fundamental da Álgebra. Em 1801, publicou Disquisitones Arithmeticae, seu tratado sobre a Teoria dos Números. No mesmo ano, calculou a órbita da asteróide Ceres. Com base em uma teoria que desenvolveu, previu corretamente onde e quando o Ceres deveria reaparecer. Morreu em 23 de fevereiro de 1855, sendo considerado o "Príncipe da Matemática".

Vejam abaixo, a resolução proposta por Gauss (isso aos 10 anos de idade):

Fonte: www.exatas.mat.br/curiosidades.htm

Desafio para NÍVEL 1 (5ª e 6ª série) e NÍVEL 2 (7ª e 8ª série)

Responda, justifique e comente:

O problema do ovo

Você quer cozinhar um ovo em dois minutos. Entretanto, você só possui dois relógios de areia (ampulheta), um de 5 minutos e outro de 3 minutos. Como você poderia colocar o ovo para cozinhar e tirá-lo dentro de 2 minutos exatos?

Fonte: minhas anotações.

Curiosidade: Multiplicação interessante!

Neste vídeo, anexado a seguir, é apresentado um novo método para a multiplicação. Vale a pena conhecer.

Site: http://video.google.com/videoplay?docid=-7641672822830464405#docid=6875218805046478830

Desafio para NÍVEL 1 (5ª e 6ª série) e NÍVEL 2 (7ª e 8ª série)

Responda, justifique e comente:

O problema das meias

Numa gaveta há 8 meias amarelas e 10 meias vermelhas. Supondo que esteja escuro e você não possa acender a luz, qual é o menor número de meias que você deve retirar da gaveta, para garantir a retirada de um par de meias da mesma cor?

Fonte: minhas anotações.

Curiosidade: Dicionário matemático!

A seguir, são apresentados alguns símbolos utilizados em Matemática.

Símbolo: /
Nome: divisão

Explicação: Lê-se como "dividido".

Exemplo: 6/2 = 3, significa que se dividirmos 6 por 2 vai dar 3.

Símbolo:

Nome: infinito

Explicação: o "oito deitado" representa o infinito. Este símbolo foi criado pelo matemático inglês John Wallis (1616-1703) para representar a "aritmética Infintorum"

Símbolo:

Nome: número pi

Explicação: o número pi é definido como sendo a razão entre a circunferência de um círculo e o seu diâmetro. Mas este número tem outras personalidades. É também um número irracional e um número transcedente. Esse número é igual a 3,141592653...

Fonte: minhas anotações.

Desafio para NÍVEL 1 (5ª e 6ª série) e NÍVEL 2 (7ª e 8ª série)

Resolva, justifique e comente:

O problema do velho e do rio

Um velho devia passar de uma para a outra margem de um rio: um cachorro, uma galinha e um maço de couves. Ele só conseguiu encontrar uma embarcação que comportava ele próprio e um dos seus pertences. O velho logo percebeu que não podia deixar sozinhos, numa das margens do rio, o cachorro e a galinha. Nem a galinha e o maço de couves. Como poderia o velho atravessar pelo rio os seus pertences com segurança?

Fonte: minhas anotações.

Curiosidade: Música de insentivo!

Essa músicas foi postada no site da UNB para professores de Matemática participantes do programa GESTAR II. Espero que gostem!

Estudar pra valer: http://www.megaupload.com/?d=JW2EMAQ2

(Após clicar no lik acima, para acessar o documentos, preencha o "Digite isso aqui", clique no "Baixar arquivo" e, por último, clique em "Download comum")

Desafio para NÍVEL 2 (7ª e 8ª série)

Responda, justifique e comente:

Duplicando o diâmetro de um círculo, a área do novo círculo:

a) ( ) duplica
b) ( ) aumenta 3,14 vezes
c) ( ) quadruplica
d) ( ) aumenta 200%

Fonte: minhas anotações.

Desafio para NÍVEL 1 (5ª e 6ª série)

Responda e comente:

A palavra "algarismo":

a) ( ) É derivada da expressão "algum ritmo", devido ao modo ritmado com que fazemos cálculos

b) ( ) Tem sua raiz no nome do matemático árabe Al-Khwarizmi, que escreveu um dos primeiros tratados de álgebra

c) ( ) Provém do termo "algaravia", que significa "linguagem confusa e ininteligível"

d) ( ) Foi criada por um grupo de alunos que consideravam seu professor de matemática um "algoz"

Fonte: minhas anotações.

Curiosidade: Matemática no cinema!

Vários filmes trazem a Matemática como temática. Seguem alguns deles:

• Quebrando a banca (EUA, 2008), de Robert Luketic
• A Prova (EUA, 2005), de John Madden
• Uma mente brilhante (EUA, 2005), de Ron Howard
• Enigma (EUA, 2001), de Michael Apted
• Pi (EUA, 1988), de Darren Aronofsky
• Gênio Indomável (EUA, 1997), de Gus Van Sant
• Cubo (Canadá, 1997), de Vincenzo Natali

Fonte: www.rerbiriosidades.com/2010/02/matematica-no-cinema.html

Desafio para NÍVEL 2 (7ª e 8ª série)

Responda, justifique e comente:

Considere um triângulo cujos lados meçam 3 cm, 6 cm e 2 cm.

a) ( ) O perímetro é igual a 11 cm
b) ( ) A medida da área é (3x6)/2 cm quadrados
c) ( ) É um triângulo retângulo porque satisfaz a relação de Pitágoras
d) ( ) Esse triângulo não existe

Fonte: minhas anotações.

Desafio para NÍVEL 1 (5ª e 6ª série)

Responda, justifique e comente:

Gato e meio come rato e meio em um minuto e meio. Quantos ratos comem um gato em um minuto?

a) 2/3 de um rato

b) 1 rato

c) 3/2 de rato

d) 2 ratos

Fonte: minhas anotações.

Curiosidade: Dívidas quitadas!

Um viajante chega numa cidade e entra num pequeno hotel.

O mesmo saca duas notas de R$ 100,00, põe no balcão e pede para ver um quarto.

Enquanto um viajante inspiciona os quartos, o gerente do hotel sai correndo com as duas notas de R$ 100,00 e vai até o açougue pagar suas dívidas com o açougueiro.

Este, pega as duas notas e vai até um criador de suínos a quem deve e paga tudo.

O criador, por sua vez, pega também as duas notas e corre ao veterinário para liquidar sua dívida.

O veterinário, com as duas notas em mãos, vai até a zona pagar o que devia a uma prostituta.

A prostituta sai com o dinheiro em direção ao hotel, lugar onde, as vezes, levava seus clientes e que ultimamente não havia pago pelas acomodações, avisa ao gerente que está pagando a conta, e coloca as notas em cima do balcão.

Nesse momento, o gringo retorna dos quartos, pega as duas notas de volta, agradece e diz não ser o que esperava e sai do hotel e da cidade.

Ninguém ganhou nenhum vintém, porém agora toda a cidade vive sem dívidas e com o crédito restaurado, e começa a ver o futiro com confiança.

O que achou?

Fonte: www.humornaciencia.com.br/blog/2009/09/matematica-interessante acessado no dia 26/04/2010.

Desafio para NÍVEL 2 (7ª e 8ª série)

Resolva e depois veja no vídeo anexado a solução:

Seja n=9867. Se você calculasse n ao cubo menos n ao quadrado você encontraria um número cujo algarismo da unidade é: (a) 0 ......... (b) 2 .......... (c) 4 .......... (d) 6 ......... (e) 8

Solução:

Fonte: http://www.orm.mtm.ufsc.br/ nos links Treinamentos e Video-treinamentos acessado no dia 26/04/2010.

Desafio para NÍVEL 1 (5ª e 6ª série)

Resolva e depois veja no vídeo anexado a solução:

A prefeitura de uma certa cidade fez uma campanha que permite trocar 4 garrafas de 1 litro vazias por uma garrafa de um litro cheia de leite. Até quanto litros de leite pode obter uma pessoa que possua 43 dessas garrafas vazias?

Solução:

Fonte: http://www.orm.mtm.ufsc.br/ nos links Treinamentos e Video-treinamentos acessado no dia 26/04/2010.

Curiosidade: um desafio!

Distribuir os números de 1 a 9 dentro dos pontos brancos (de intersecção), sem repetir, de forma que a soma dos números pertencentes à circunferência exrterna seja exatamente igual à soma dos números pertencentes a cada uma das circunferências internas.

Fonte: RPM - OBMEP

Desafio para NÍVEL 1 (5ª e 6ª série) e NÍVEL 2 (7ª e 8ª série)

Tente! E nos comunique pelo comentários.

Instruções

• em cada linha há 5 números e um sexto número, chamado "total".
• coloque os sinais +, -, x, : e parênteses, colchetes, chaves, de modo que o resultado das contas indicadas seja o "total".
• os 5 números devem ser usados, cada um deles uma só vez, em qualquer ordem.

Exemplo: 7, 8, 1, 9, 9 total: 16. Uma solução: (9:9)x(7+8+1)=16.

Agora é sua vez!

1. 1, 5, 3, 6, 10 com total 5
2. 8, 11, 9, 1, 8 com total 2
3. 11, 10, 15, 20, 3 com total 6
4. 12, 18, 3, 11, 12 com total 8
5. 4, 16, 10, 24, 25 com total 1
6. 17, 14, 7, 17, 13 com total 7
7. 2, 9, 5, 9, 4 com total 22
8. 3, 6, 10, 5, 7 com total 2
9. 8, 6, 11, 5, 21 com total 7
10. 6, 1, 2, 2, 17 com total 8

Fonte: adaptado do artigo Atividades em sala de aula de Renate Watanabe, RPM 61.

Curiosidade: Fractal

Um fractal é uma forma geométrica que pode ser subdividida em partes menores, sendo que cada uma dessas partes é uma cópia reduzida da forma inteira.

Muitas estruturas matemáticas são fractais, e através delas consegue-se obter imagens irregulares e fragmentadas, muitas delas impressionantes por sua complexidade e beleza.

Formas fractais também estão presentes na Natureza e podem ajudar a descrever muitos objetos do mundo real que não correspondem a formas geométricas simples, como nuvens, montanhas, costas litorâneas e a turbulência do ar.

Fonte: www.sitedecuriosidades.com/ver/fractal.html acessado no dia 22/04/2010.

Alguns fractais:

Desafio para NÍVEL 2 (7ª e 8ª série)

Responda, justifique e mostre no comentários:

Fonte: www.tutorbrasil.com.br/estudo_matematica_online/obm/teoria_dos_números.php acessado no dia 22/04/2010.

Desafio para NÍVEL 1 (5ª e 6ª série)

Responda, justifique e mostre no comentários:

No quadrado mágico abaixo, a soma dos números em cada linha, coluna e diagonal é sempre a mesma. Por isso, qual deve ser o valor a ser colocado no lugar do x?

Fonte: www.tutorbrasil.com.br/estudo_matematica_online/obm/teoria_dos_numeros.php acessado no dia 22/04/2010.